反函数是一个数学概念，它描述了函数的逆操作。对于一个函数f，如果存在另一个函数g，使得对于所有的x，都有gqwe2 = x和fqwe2 = x，那么g就是f的反函数，通常记作f^。

反函数的存在条件是函数f必须是双射的，即每个输入x对应唯一的输出y，并且每个输出y对应唯一的输入x。这样，函数f才能有唯一的逆函数g。

反函数在数学、物理、工程等领域都有广泛的应用。例如，在求解方程时，我们经常需要使用反函数来将方程转化为易于求解的形式。在图像处理中，反函数可以用来恢复原始图像。在密码学中，反函数可以用来加密和解密信息。

需要注意的是，并不是所有的函数都有反函数。例如，对于函数f = x^2，它不是双射的，因为对于同一个输出y，存在两个不同的输入x（即x和x），所以它没有反函数。亲爱的数学迷们，今天我们要来聊聊一个听起来有点神秘，但实际上却非常实用的数学概念——反函数。想象你手中有一张地图，上面标注了从A点到B点的所有路径。现在，你想要知道从B点回到A点的路怎么走，这时候，反函数就像是一把神奇的钥匙，能帮你解锁这个谜题。准备好了吗？让我们一起踏上这场数学探险之旅吧！

什么是反函数？

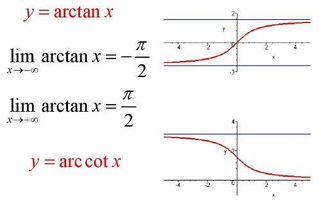
反函数，简单来说，就是原函数的“倒影”。它就像一面镜子，将原函数的输入和输出互换位置。举个例子，假设你有一个函数f(x)，它将x映射到y，即y = f(x)。那么，反函数g(y)就会将y映射回x，即x = g(y)。是不是感觉有点像玩捉迷藏呢？

反函数的诞生

反函数并不是凭空出现的，它有着悠久的历史。早在17世纪，数学家们就开始探索这个概念。到了18世纪，瑞士数学家欧拉更是对反函数进行了深入研究，奠定了它作为数学领域重要概念的基础。

反函数的应用

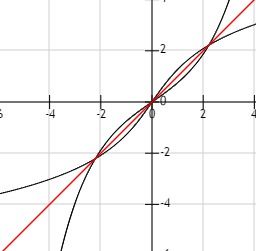
反函数的应用范围非常广泛，从物理学到经济学，从工程学到计算机科学，几乎无处不在。以下是一些典型的应用场景：

1. 物理学：在物理学中，反函数常用于求解物理量之间的关系。比如，在电磁学中，我们可以利用反函数来计算电场强度。

2. 经济学：在经济学中，反函数可以帮助我们分析市场供需关系。例如，我们可以通过反函数来预测商品价格的变化。

3. 工程学：在工程学中，反函数可以用于设计复杂的系统。比如，在建筑设计中，我们可以利用反函数来计算建筑物的结构稳定性。

4. 计算机科学：在计算机科学中，反函数可以用于算法优化。例如，在图像处理中，我们可以利用反函数来提高图像质量。

如何求解反函数？

求解反函数并不是一件容易的事情，但只要掌握了正确的方法，就能轻松应对。以下是一些求解反函数的步骤：

1. 确定原函数的定义域和值域：这是求解反函数的基础。

2. 交换原函数的自变量和因变量：将原函数f(x)中的x和y互换，得到y = f(x)。

3. 解出y关于x的表达式：这一步是求解反函数的关键。

4. 确定反函数的定义域：根据原函数的值域和求解过程中可能出现的限制条件，确定反函数的定义域。

反函数的局限性

虽然反函数在许多领域都有广泛的应用，但它也有一些局限性。以下是一些需要注意的地方：

1. 原函数必须是单调函数：只有单调函数才有反函数。

2. 反函数可能不是初等函数：有些反函数可能无法用简单的数学表达式表示。

3. 反函数的定义域和值域可能有限制：在某些情况下，反函数的定义域和值域可能受到限制。

反函数，这个看似神秘的数学概念，其实在我们的生活中有着广泛的应用。通过今天的分享，相信你已经对反函数有了更深入的了解。让我们一起继续探索数学的奥秘，发现更多有趣的知识吧！